| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- PSR
- 주식초보
- 통화정책
- 미시경제
- 종합주가지수 개념
- 합명회사
- 무차별곡선 #한계효용 #한계효용 균등의 법칙 #한계효용 체감의 법칙 #예산선 #미시경제
- 유동성함정
- 개념용어
- 토익스피킹
- TOEIC specking
- 미시경제 #조건부상품
- TOEIC Speaking
- 빅맥지수 #Big mac Index
- 가격상한제
- 공모주
- 토스
- 가격하한제
- 재정정책
- 노동공급결정 #사회복지제도 #소비저최적선택이론
- 주식
- 유한회사
- ROE
- 이코노미
- 주가의 종류
- 전세상한제
- 미시경제 #기대효용이론 #확실성등가 #리스크프리미엄
- IS-LM
- 합자회사
- 양적완화 #헬리콥터머니 #quantitative easing
- Today
- Total
프라하또가고싶다
13. 불확실성과 기대효용이론 본문
저번 글에서는 불확실성과 조건부상품에 대해서 다뤘었다. 조건부상품이란 불확실성이 존재한다는 가정하에 두가지 선택지에서 어떠한 선택을 했을 시 서로 결과값이 달라지는 조건부적 상황에 대한 선택의 문제다.
기대효용이론이란 불확실성이 존재하는 상황에서 여러 선택지가 있을 시 기대효용의 극대화를 추구하는 소비자의 선택모형으로 접근하는 방식이다.
기대효용이론
현실에서는 선택지가 딱 두가지인 경우는 매우 적다. 대게 불확실성하의 선택은 두가지 이상의 가능한 상황이 결부된 경우가 많다. 따라서 폰 노이만과 모겐스턴은 기대효용이론을 활용하여 각각의 선택을 분석했다. 즉 합리적인 의사결정자는 기대효용을 극대화하는 결정을 갖는다는 했다.
기대효용,EU(W)이란, 불확실성하에서 어떤 선택에 따른 주관적인 효용을 의미한다. 그러나 사람마다 위험에 대한 성향이 다르기 때문에 효용의 크기는 각각 다르다.
EU(W)=P(확률)*Wf + (1-P)*Wn
기대값,(EW)이란, 기대가치로 설명하다. 불확실성하에서 여러 확률에 따라 예상되는 가치의 크기다.
E(W)=P*Wf + (1-P)*Wn
기대효용이론의 가정 5가지
1. 완비성 2. 연속성 3. 독립성 4. 부등확률 5. 복합확률
<예제>
당첨될 확률 0.01로 만년필(10,000원)을 상으로 받는다. 그리고 0.99의 확률로 볼펜(100원)을 받는다.
그렇다면 현재 상황에서 기대효용과 기대값을 구해보자.
만년필의 효용은 1000이고 볼펜의 효용은 1이다.
기대효용
EU(W)=0.01*1000+0.99*1
=10+0.99
EU(W)=10.99
기대값
E(W)=0.01*10000+0.99*100
=100+99
E(W)=199
위의 식을 일반화 한다면...
기대값
EV=P*W1 + (1-P)*W2
기대효용
U(L)=P*U(W1) + P*U(W2)
<예제2>
2500만원의 이득과 관련해 의사결정자에게 P의 확률로 10억원의 이득을 얻고, (1-P)의 확률로 2억원의 손실을 보는 경우와 확실하게 2500만원의 이득을 얻는 경우 사이에서 효용의 차이를 느끼지 못하는 확률값P의 값이 얼마인가? 이때 10억원의 효용은 100, -2억원의 효용수준은 0이라 가정한다.
st)P는 0.4이다.

위와 같이 폰노이만-모겐스턴 효용함수를 통해서 그래프와 곡선을 도출해낼 수 있다.
이러한 상황에서 일반적인 사람들은 오목한 형태의 곡선을 갖고 있다. 반면에 위험중립형인 사람은 아래의 보라색 직선과 같다. 위험추구적인 사람은 그래프에서 아래의 붉은 곡선과 같은 형태를 띈다.

Risk Premium 과 확실성등가
리스크 프리미엄(RP)란 불확실한 재산을 확실한 재산으로 바꾸기 위해 투자자가 최대한 지불할 용의가 있는 금액을 의미한다.
EW-W*
확실성등가란 불확실한 재산과 동일한 가치가 있는 확실한 재산을 의미한다.
W* = EW - RP
<예제3>
어떠한 복권이 있는데, 70%의 확률로 100만원을 주고, 30%의 확률로 400만원을 준다. 그런데 이워비의 폰노이만-모겐스턴 효용함수가 다음과 같이 주어져 있다고 한다.
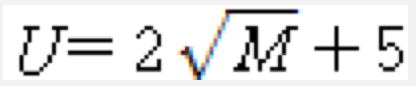
Q1. 이 복권이 이워비에게 주는 효용의 크기는 얼마인가
Q2. 이 복권의 상금의 기대치를 확실하게 받는다면 그 효용은 얼마인가?
Q3. 위의 계산 결과에 기초해, 이 복권과 관련된 위험프리미엄을 계산하라.


'공부 > 미시, 거시' 카테고리의 다른 글
| 15. 거시경제의 역사 (0) | 2020.04.06 |
|---|---|
| 14. 생산함수 (0) | 2020.04.06 |
| 12. 불확실성과 조건부상품 (0) | 2020.04.05 |
| 11. 지수이론(라스파이레스, 파쉐) (0) | 2020.04.04 |
| 10. 기펜재(Giffen good)란? (0) | 2020.04.03 |




